Apprendre à inhiber : un enjeu pour surmonter des erreurs systématiques en mathématiques
- Le21duLaPsyDÉ

- 21 févr. 2022
- 20 min de lecture
Dernière mise à jour : 20 avr. 2022

Les mathématiques sont fondamentales dans de nombreuses situations de notre vie quotidienne telles que faire des courses, gérer un agenda, calculer un pourboire, faire de la cuisine, mais aussi jouer à des jeux de société avec des dés. L’apprentissage des mathématiques reste complexe pour les élèves français comme le démontre année après année les résultats des études PISA [1]. Il y a donc un enjeu à développer des interventions en classe qui permettent d’aider les élèves à surmonter les obstacles cognitifs qu’ils peuvent rencontrer au cours de leurs apprentissages des mathématiques. Comme nous l'avons vu dans les articles précédents du 21 du LaPsyDÉ [2], [3], l'inhibition joue un rôle crucial dans le développement de certaines compétences mathématiques, pour le développement précoce du nombre ou le calcul mental par exemple. L’enjeu de cet article est de montrer que des interventions pédagogiques qui visent à enseigner aux élèves à identifier les problèmes pièges et à leur apprendre à inhiber l’automatisme trompeur est un levier pédagogique pour aider les élèves à surmonter des difficultés systématiques qu’ils peuvent rencontrer en mathématiques.
1. Inhibition et mathématiques
a) Les compétences numériques préscolaires
Comme nous l'avons vu dans l’article publié par le 21 du LaPsyDÉ intitulé "Développer son attention vers le nombre", l'inhibition joue un rôle crucial dans le développement du système approximatif du nombre précoce (préscolaire) [2].
La tâche de conservation du nombre est un bon exemple du rôle que peut jouer l’inhibition dans la construction du concept de nombre chez l’enfant. Dans la tâche de conservation du nombre, inventée par Jean Piaget, on présente une rangée de jetons à l’enfant et on lui demande d’en créer une deuxième pareille. Vers 4-5 ans, l’enfant est capable de créer une rangée de même longueur avec le même nombre de jetons. On vérifie que l’enfant accepte l’équivalence initiale en lui demandant s’il y en a autant dans les deux rangées. Ensuite, l’expérimentateur écarte les jetons dans une des deux rangées (c’est la phase de transformation) et repose la même question à l’enfant. Et là surprise, les enfants après transformation de la longueur d’un des deux alignements considèrent qu’il y en a plus dans la rangée la plus longue (voir Fig 1). Les erreurs que commettent les élèves de moins de 7 ans dans cette tâche proviennent en partie du fait qu’ils utilisent une stratégie automatique, rapide et très efficace (en psychologie on appelle cela une heuristique) mais qui est trompeuse dans ce contexte. Cette stratégie, c’est l’heuristique « longueur égale nombre ». Le cerveau de l’enfant détecte très tôt cette régularité visuelle et spatiale et la renforce car elle marche très bien dans un grand nombre de situations. Et nous continuons à l’utiliser toute notre vie. Pensez par exemple à la façon dont vous choisissez la file que vous allez emprunter quand vous arrivez à un péage sur l’autoroute. Très rapidement en comparant la longueur des alignements de voiture vous vous dirigez vers la file la plus courte sans avoir compté les voitures. Et vous avez dû vous rendre compte que cette heuristique ne fonctionne pas toujours. Dans notre cerveau, nous avons aussi à notre disposition des algorithmes exacts, des stratégies analytiques et délibératives, comme le comptage. Pour réussir la tâche de conservation du nombre, il faut non seulement être capable d’inhiber l’heuristique « longueur égale nombre », trompeuse dans ce contexte, mais aussi d’activer par la suite un algorithme de comptage qui permet par exemple de se rendre compte que même si les jetons dans une des deux rangées ont été écartés, il y en a toujours le même nombre dans la rangée du haut et du bas [4].
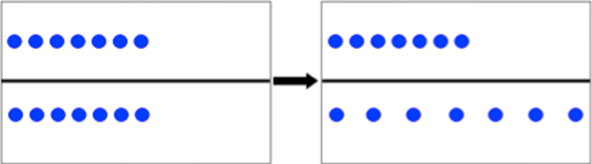
Figure 1: Exemple d'un essai dans la tâche de conservation du nombre.
b) Compétences numériques à l'école
Comme nous l'avons vu dans l’article publié par le 21 du LaPsyDÉ intitulé "Comment mon cerveau apprend-il les mathématiques ?", le rôle crucial de l'inhibition en mathématiques ne se limite pas au traitement approximatif du nombre [3]. L’inhibition est essentielle pour tous les apprentissages en mathématiques car certaines heuristiques se construisent au cours de l’acquisition de certaines notions qui interfèrent plus tard avec l’acquisition de notions plus complexes.
Prenons l’exemple des nombres décimaux et des difficultés rencontrées par les élèves à comparer des nombres décimaux quand le nombre le plus petit (1,456) a plus de chiffres après la virgule que le nombre le plus grand (1,5). Les élèves commettent des erreurs systématiques car ils ont tendance à utiliser une heuristique du type « plus il y a de chiffres, plus le nombre est grand » ce qui les amène à penser que 1,456 est plus grand que 1,5. Cette heuristique s’est très probablement mise en place au cours de l’apprentissage de la comparaison des nombres entiers. Bien qu’on enseigne aux élèves à comparer le chiffre des unités, puis des dizaines, puis des centaines pour comparer deux nombres entiers, très rapidement leur cerveau détecte que plus il y a de chiffres dans un nombre entier, plus il est grand. Cette heuristique est très rapide et efficace dans le contexte de la comparaison des nombres entiers mais devient trompeuse quand les élèves commencent à comparer des nombres décimaux. Au laboratoire [6], nous avons démontré expérimentalement que les élèves de CM1 et de CM2 mais aussi les adultes doivent inhiber l’heuristique « plus il y a de chiffres, plus le nombre est grand » pour comparer des nombres décimaux quand le nombre le plus petit (1,456) a plus de chiffres après la virgule que le nombre le plus grand (1,5).
Au cours de l’apprentissage des fractions, un phénomène similaire s’observe. Les élèves ont des difficultés pour comparer des fractions qui ont les mêmes numérateurs (1/7 vs 1/3). Ils ont tendance à considérer qu’un 1/7 est plus grand qu’1/3 car ils utilisent l’heuristique "plus le nombre entier est grand, plus la fraction est grande". Cette heuristique s’est construite et renforcée au cours de l’apprentissage de la comparaison des fractions avec les mêmes dénominateurs : quand les élèves comparent 5/9 et 7/9, il leur suffit de comparer les numérateurs pour identifier la fraction la plus grande. Comme pour la comparaison des nombres décimaux, nous avons démontré que des élèves au collège et des étudiants à l’université doivent inhiber l’heuristique "plus le nombre entier est grand, plus la fraction est grande " pour comparer des fractions avec les mêmes numérateurs [7].
Nous avons également démontré au laboratoire que l’inhibition jouait un rôle dans la capacité à résoudre des problèmes arithmétiques à contenus verbaux. Quand les élèves de CM1 et de CM2 commencent à résoudre un problème du type « Pierre a 25 billes. Il a 5 billes de moins que Luc. Combien de billes a Luc ? », ils ont tendance à utiliser l’heuristique "additionner si plus, soustraire si moins” et en conclure que Luc a 20 billes. Cette heuristique fonctionnait très bien jusque-là dans des problèmes plus simples et s’est donc renforcée. Nous avons montré au laboratoire que des élèves de CM1 et CM2, des étudiants en première année de lettres et même des étudiants en master de mathématiques doivent inhiber l’heuristique trompeuse "additionner si plus, soustraire si moins”, pour résoudre correctement ce type de problèmes arithmétiques [8].
Ces découvertes suggèrent que l’inhibition des heuristiques trompeuses est un facteur important de l’acquisition de certaines notions en mathématiques. Elles doivent nous amener à réinterroger le statut de ces erreurs systématiques observées dans les situations pièges ou problèmes : ces erreurs ne relèvent pas d’un manque de connaissances de l'élève, mais elles reflètent plus certainement une difficulté à inhiber certaines heuristiques fortement ancrées dans le cerveau de l’élève. La question qui s’est naturellement posée pour les chercheurs du laboratoire a été de déterminer quelle approche pédagogique fonctionnerait le mieux dans ces contextes pièges pour aider les élèves à surmonter leurs difficultés.
2. Apprendre à inhiber des heuristiques trompeuses ?
Au laboratoire LaPsyDÉ, nous sommes en train de tester scientifiquement l’efficacité d’un apprentissage à l’inhibition, appelé aussi apprentissage méta-exécutif car il implique non seulement une fonction exécutive, l’inhibition, mais aussi des processus métacognitifs permettant aux élèves de prendre conscience des stratégies qu’ils utilisent dans plusieurs situations pièges et problèmes. Cette intervention méta-exécutive est basée sur la théorie des trois systèmes du développement cognitif et des apprentissages, proposée par Olivier Houdé (voir Box 1, [9]) et a déjà démontré son efficacité pour aider des étudiants à surmonter des erreurs systématiques de raisonnement dans lesquelles une heuristique doit être inhibée car elle interfère avec l’algorithme [10].
Box 1. La théorie des trois systèmes cognitifs
Théorie mise en avant par Pr. Houdé, cette théorie postule l’existence d’un modèle de pensée à trois systèmes. Le système 1 est celui des heuristiques, le système 2 est celui des algorithmes et le troisième système est celui de l’inhibition (Fig 2.). Ce système 3 aurait une fonction d’arbitrage lorsque les deux autres systèmes entrent en conflit, permettant d’interrompre le système 1 et d’activer le système 2, pour aboutir à la bonne réponse.
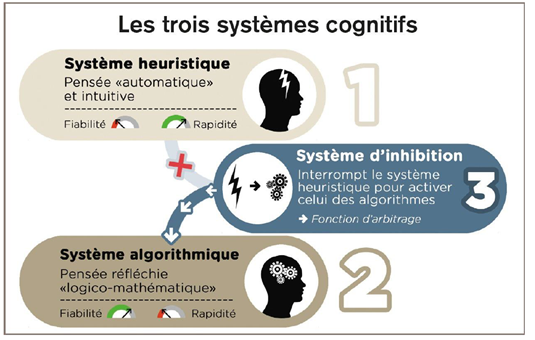
Figure 2 : Illustration des trois systèmes cognitifs où le système d’inhibition permet d’interrompre le système heuristique, au profit du système algorithmique.
Reprenons l’exemple des nombres décimaux. Lorsque des élèves de CM1 et de CM2 apprennent à comparer des décimaux, ils vont avoir tendance à répondre que 1,852 est plus grand que 1,87 car ils appliquent erronément l’heuristique « plus il y a de chiffres après la virgule, plus le nombre est grand ». C’est à ce moment critique de l’apprentissage des nombres décimaux qu’une intervention pédagogique visant à apprendre aux élèves à identifier le piège, l’heuristique trompeuse et à l’inhiber peut s’avérer utile pour eux.
Cette intervention pédagogique se déroule en 3 phases :
1. D’abord, on alerte les élèves sur le piège à éviter en leur expliquant, par exemple :
« Attention, dans certains cas il est difficile de comparer des nombres décimaux. Par exemple, lorsqu’on compare 1,87 et 1,852 certains enfants disent que 1,852 est plus grand que 1,87. Ils se trompent parce qu’ils ont l’habitude de dire que le nombre le plus grand est celui qui a le plus de chiffres. Cette habitude peut t’influencer dangereusement. On croit que ça nous aide de regarder le nombre décimal qui contient le plus de chiffres alors qu’en fait on tombe dans un piège. »
2. Ensuite, on rappelle aux élèves la règle à suivre, en continuant l’explication :
« Pour dire qu’un nombre décimal est plus grand qu’un autre, il faut faire attention à comparer les chiffres des unités entre eux, les chiffres des dixièmes entre eux, les chiffres des centièmes entre eux et les chiffres des millièmes entre eux. Pour notre exemple 1,852 et 1,87, on remarque que les chiffres des centièmes sont différents. Ici, 1,852 est plus petit que 1,87 car le chiffre des centièmes 5 est plus petit que 7. »
3. Pour terminer l’apprentissage, on propose aux élèves une phase de manipulation à l’aide de l’attrape-piège (Fig. 3). Il s’agit d’une planche transparente dont la partie hachurée représente l’inhibition à exercer contre l’heuristique et le cercle central ajouré représente la bonne stratégie de réponse. Les élèves disposent de deux cartons réponses pour cette phase :
- La mauvaise réponse produite par l’heuristique (ex : 1,87 plus petit que 1,852). Les élèves sont invités à l’identifier et à la placer sous les hachures de manière à inhiber l’heuristique et éviter le piège.
- La bonne réponse produite par l’algorithme (ex : 1,87 plus grand que 1,852). Les élèves sont invités à l’identifier pour la placer ensuite dans le cercle ajouré, qui représente l’activation de la bonne stratégie.
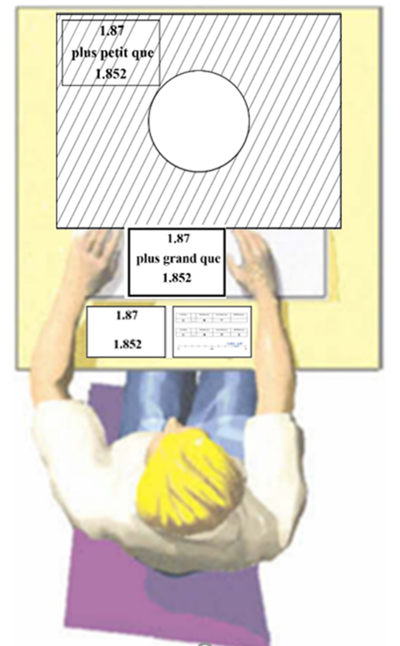
Figure 3 : L’attrape-piège
3. Comment avons-nous démontré l'efficacité de cette intervention ?
Nous avons utilisé une méthode classique en psychologie des apprentissages : évaluation (pré-test) – intervention – évaluation (post-test). Nous avons donc demandé à des élèves de CM1 et de CM2, avant de leur proposer une intervention pédagogique, de participer à une évaluation en groupe classe pour mesurer leurs capacités à comparer des nombres décimaux. Ensuite, nous avons aléatoirement réparti les élèves dans deux groupes :
- Un groupe qui suit l’apprentissage méta-exécutif présenté ci-dessus.
- Un groupe qui suit un autre type d’apprentissage (condition contrôle ou témoin). Au cours de cette intervention pédagogique, on enseigne aux élèves la règle (l’algorithme) de comparaison des nombres décimaux. On commence donc l’intervention directement à la phase 2 présentée ci-dessus. Dans la phase 3 de l’intervention, la phase de manipulation, les participants n’utilisent pas l’attrape-piège mais seulement une planche séparée en deux par une ligne. Les participants sont invités à placer au-dessus de la ligne le carton bonne réponse et en dessous de la ligne le carton mauvaise réponse.
Deux semaines après l’intervention, nous avons de nouveau évalué en groupe classe les capacités à comparer des nombres décimaux. Les élèves qui suivent un apprentissage méta-exécutif progressent plus entre le prétest et le posttest que les élèves du groupe contrôle, ce qui démontre l’efficacité d’une approche pédagogique consistant à enseigner aux élèves comment identifier le piège, et comment inhiber l’heuristique trompeuse [11].
Au laboratoire, nous essayons de généraliser ce premier résultat à d’autres situations pièges pour démontrer l’efficacité de cette approche :
- Pour la résolution de problèmes arithmétiques à contenus verbaux [12], en enseignant aux élèves âgés de 7 à 10 ans à inhiber l’heuristique « additionner si plus, soustraire si moins » lorsqu’ils ont à résoudre des problèmes du type : « Pierre a 25 billes. Il a 5 billes de moins que Luc. Combien de billes a Luc ? »
- Pour l’acquisition de la conservation du nombre [13], en enseignant aux élèves âgés de 4 à 6 ans à inhiber l’heuristique « longueur égale nombre » lorsqu’ils effectuent la tâche de conservation du nombre.
- Pour la comparaison de fraction avec les mêmes numérateurs (ex :1/7 vs 1/3) en enseignant aux élèves au début du collège à inhiber l’heuristique “plus le nombre entier est grand, plus la fraction est grande”.
- Pour éviter certaines erreurs d’attraction dans la conjugaison des verbes (ex : « je les manges ») en enseignant aux élèves à inhiber l’heuristique « après les, je mets un “s” ».
Pour aller plus loin:
[1] Organization for Economic Co-operation and Development (2003). The PISA 2003 assessment framework-mathematics, reading, science and problem-solving knowledge and skills. Paris: Author.
[2] 21 du LaPsyDÉ. (2021). Développer son attention vers le nombre https://www.le21dulapsyde.com/post/d%C3%A9velopper-son-attention-vers-le-nombre
[3] 21 du LaPsyDÉ. (2021). Comment mon cerveau apprend-il les mathématiques ?. https://www.le21dulapsyde.com/post/comment-mon-cerveau-apprend-il-les-mathématiques
[4] Houdé, O., Pineau, A., Leroux, G., Poirel, N., Perchey, G., Lanoë, C., Lubin, A., Turbelin, M.R., Rossi, S., Simon, G. and Delcroix, N., 2011. Functional magnetic resonance imaging study of Piaget’s conservation-of-number task in preschool and school-age children: A neo-Piagetian approach. Journal of experimental child psychology, 110(3), pp.332-346.
[5] Vamvakoussi, X., & Vosniadou, S. (2010). How many decimals are there between two fractions? Aspects of secondary school students’ understanding of rational numbers and their notation. Cognition and instruction, 28(2), 181-209.
[6] Roell, M., Viarouge, A., Hilscher, E., Houdé, O., & Borst, G. (2019). Evidence for a visuospatial bias in decimal number comparison in adolescents and in adults. Scientific reports, 9(1), 1-9.
[7] Rossi, S., Vidal, J., Letang, M., Houdé, O., & Borst, G. (2019). Adolescents and Adults Need Inhibitory Control to Compare Fractions. PsychArchives. https://doi.org/10.23668/psycharchives.2381
[8] Lubin, A., Rossi, S., Lanoë, C., Vidal, J., Houdé, O., & Borst, G. (2016). Expertise, inhibitory control and arithmetic word problems: A negative priming study in mathematics experts. Learning and Instruction, 45, 40-48.
[9] Houdé, O. (2019). 3-system theory of the cognitive brain: A post-Piagetian approach to cognitive development. Routledge.
[10] Houdé, O. et al. Shifting from the perceptual brain to the logical brain: the neural impact of cognitive inhibition training. J. Cogn. Neurosci. 12, 721–728 (2000).
[11] Hilscher, E., Létang, M., Roell, M., Viarouge, A., Houdé, O., & Borst, G. (en révision). Improving decimal number comparison in school-age children by teaching how to inhibit a misleading strategy. Science of learning.
[12] Létang, M., Citron, P. Garbarg-Chenon, J., Houdé, O., & Borst, G. (en revision). Learning to inhibit a misleading strategy to overcome difficulties with arithmetic word problems in the classroom : Converging evidence from a laboratory and citizen research studies. Learning and instructions.
[13] Létang, M. & Garbarg-Chenon, J. (2020). Entraîner le cerveau à résister – Coffret Non-lecteurs. Nathan
Auteurs :

Margot Roell
Post-doctorante au LaPsyDÉ, Université de Paris

Emma Hilscher
Doctorante au LaPsyDÉ, Université de Paris
É

Grégoire Borst
Directeur du LaPsyDÉ & Professeur de Psychologie du développement et de Neurosciences cognitives de l'éducation, Université de Paris

English version
Learning to inhibit: a crucial challenge to overcome systematic errors in mathematics

Mathematics is fundamental in a great number of situations of our daily life such as going shopping, managing a diary, calculating a tip in a restaurant, but also playing a board game. However, learning mathematics is still a complex feat for French students as shown year after year by the result of the PISA reports [1]. Developing school-based interventions to help students overcome cognitive obstacles that they may face over the course of their mathematical learning is, thus, essential. As discussed in previous articles of the 21 du LaPsyDÉ (2, 3), inhibition has a crucial role in the development of mathematical ability. Through this article we wish to show that pedagogical interventions that aim to teach children to identify deceptive problems and learn to inhibit misleading automatisms are pedagogical tools that help students overcome systematic difficulties in math.
1. Inhibition and mathematics
a) Pre-schooling numerical abilities
As seen in a previous article published by the 21 du LaPsyDÉ entitled “Developing the attention to numbers”, inhibition has been shown to have a crucial role in the development of early (pre-schooling) approximate numerical abilities [2].
The number conservation task is a good example of the role inhibition can have in the construction of the concept of number in children. In the number conservation task, invented by Jean Piaget, we present a row of tokens to the child and ask him to create a second row that is an exact replica of the first. At around 4 to 5 years, children are capable of creating a row of the same length and with the same number of tokens. We check that the children accept the initial equivalence of the rows by asking if the two rows contain the same number of tokens. Then, the experimenter spreads apart the tokens of one of the two rows (the transformation phase) and asks the same question. Surprisingly, after this transformation of the length (but not of the token number) of one of the two rows, children consider that there are more tokens in the row that is the longest (see Fig 1). The errors that children under the age of 7 commit in the conservation task come from the fact that they use an automatic strategy that is fast and very efficient (in psychology we call that a heuristic), but is misleading in this context. In the number conservation task, this strategy is the heuristic “length equals number”. The child’s brain detects early on this visual and spatial regularity and starts using it as it is very effective in a great number of situations. We continue to use this strategy throughout our life. For example, on a highway toll, when we choose which queue to go behind, we compare the length of the car alignments and we go to the shortest queue without having to count the cars. However, you must have realized that this heuristic does not always work. In our brain, we also have at our disposal exact algorithms, analytical and deliberative strategies, such as counting. In order to succeed in the number conservation task, we have to be able to inhibit the heuristic “length equals numbers”, that is misleading in this context, before activating the counting algorithm that allows us to realize that even if the tokens of one of the rows are spread apart there is the same number of tokens in both rows [4].

Figure 1: Example of a number conservation trial.
b) Numerical abilities at school
As seen in a previous article published by the 21 du LaPsyDÉ entitled “How does my brain learn mathematics”, the crucial role of inhibition in mathematics is not limited to pre-schooling approximate numerical processing [3]. Inhibition is crucial for all types of mathematical learning as certain heuristics are built along the acquisition of certain notions and may later interfere with the acquisition of more complex notions.
Let’s take the example of decimal numbers and the difficulty faced by children when they compare decimal numbers in which the smallest number (1.456) has the greatest number of digits after the decimal point than the biggest number (1.5). Children commit systematic errors as they have the tendency to use the heuristic “the greater the number of digits, the greater its magnitude”. This heuristic leads children to believe that 1.456 is greater than 1.5. This heuristic was probably established when children learned to compare whole numbers. Although teachers teach students to compare units, then the tens, then the hundreds to compare whole numbers, very quickly the brain detects that the greater the number of digits the greater the number. This heuristic is very quick and efficient when comparing whole numbers, but becomes misleading when comparing decimal numbers. In the laboratory, we have experimentally shown that grade 3 and grade 4 students but also adults need to inhibit the heuristic “greater the number of digits, the greater its magnitude” to compare decimal numbers in which the smallest number (1.456) has the greatest number of digits after the decimal point than the biggest number (1.5).
When learning fractions, a similar phenomenon can be observed. Students have difficulties comparing fractions with common numerators (1/7 vs 1/3). They tend to consider that 1/7 is larger than 1/3 as they use the “greater the whole number, the greater the fraction” heuristic. This heuristic was built and reinforced when children learned to compare fractions with the same denominator: when comparing 5/9 and 7/9 children can simply compare the numerators to identify the greater fraction. As with decimal numbers, in our lab, we have experimentally shown that both children and University students need to inhibit the “greater the whole number, the greater the fraction” heuristic in order to correctly compare fractions with the same numerator [7].
Research in our lab has also shown that inhibition plays an important role in solving arithmetic word problems. When grade 3 and grade 4 students are presented with problems such as “Peter has 25 marbles. He has 5 less marbles than Luc. How many marbles does Luc have?”, they tend to use the heuristic “add if more or subtract if less” and conclude that Luc has 20 marbles. This heuristic can be very effective for simpler arithmetic word problems and has therefore been reinforced. In our lab we have also shown that children, adults and even expert mathematicians have to inhibit the “add if more or subtract if less” heuristic in order to correctly solve such arithmetic word problems [8].
These findings suggest that inhibition of a misleading heuristic is an important factor in the acquisition of mathematical notions. They lead us to question the systematic errors observed in mathematics: these errors may not reveal a lack of knowledge of the student, but rather a difficulty to inhibit heuristics that are strongly anchored in the student’s brain. The question that naturally follows is to determine which pedagogical approach works best to help the student overcome their difficulties in these “trap” situations.
2. Learning to inhibit misleading heuristics ?
At LaPsyDÉ, we are currently scientifically testing the efficacy of an intervention based on learning through inhibition. This intervention is also known as meta-executive learning, as it implies not only an executive function (i.e., inhibition), but also metacognitive processes that allow students to realize the strategies they use in “trap” situations. This meta-executive pedagogical intervention is based on the three-system theory of cognitive development and learning (see Box 1, [9]). This intervention has already shown its efficacy in helping students overcome systematic errors in reasoning in which a heuristic must be inhibited as it interferes with the algorithm [10].
Box 1. The three-system theory
Theory put forward by Pr. Houdé, this theory stipulates the existence of a three-system thinking model. System 1 represents the intuitive heuristic process, System 2 represents logical algorithms and System 3 represents inhibition. System 3 is said to come into play when System 1 and 2 are in conflict, allowing to interrupt System 1 and activate System 2, thus achieving the correct answer. The ability to inhibit would allow us to access our logical algorithms when they are in conflict with our heuristics.
Let’s go back to the decimal number example. When students of grade 3 and 4 learn to compare decimal numbers, they frequently commit errors when the smallest decimal number has the greatest number of digits (e.g., 1.87 vs. 1.852), even if they understand the mathematical principles of the comparison of decimals. Indeed, students tend to answer that 1.852 is greater than 1.87 as they rely on the misleading heuristic ““the greater the number of digits, the greater its magnitude”. It is at this point in learning decimal numbers, that a pedagogical intervention focused on teaching students to identify and inhibit the misleading heuristic can prove useful for students.
This approach can be broken down in 3 phases:
1. First, we alert the student of the trap to avoid, for example:
“Be careful, in some cases it can be difficult to compare decimal numbers. For example, when you compare 1.87 and 1.852 certain children say that 1.852 is greater than 1.87. They err because they have a habit of considering that the greater number is the number with the most digits. This habit can be misleading. We think that it helps us to look at the decimal number which contains the most digits whilst in fact we fall into a trap!”
2. Then, we remind the student of the mathematical principle to follow by continuing the explanation:
“To be able to say that a decimal number is greater than another, we need to make sure to compare each digit between the two decimal numbers. You need to compare the unit digit with the unit digit, the tenth with the tenth, the hundredth with the hundredth. In our example, 1.852 and 1.87, the two decimal numbers are different at the hundredth digit. Here, 1.852 is smaller than 1.87 because the hundredth decimal 5 is smaller than 7.”
3. Finally, the child is able to put into practice what they were taught in the manipulation part of the intervention using the “Trap-Catcher” (Fig. 3). The trap-catcher is a simple hatched square with a non-hatched circle at its centre. These represent inhibition and activation of the correct strategy respectively. The children are then presented with two answer cards:
- The wrong answer produced by the misleading heuristic (ex : 1,87 smaller than 1,852). The children are asked to identify the wrong answer and place it in the hatched part of the “Trap-catcher” so as to inhibit the heuristic and avoid the trap.
- The correct answer produced by the mathematical principle to follow (ex : 1,87 greater than 1,852). The children are asked to identify the correct answer and place it in the non-hatched part of the “Trap-catcher”, which represents the activation of the correct strategy.
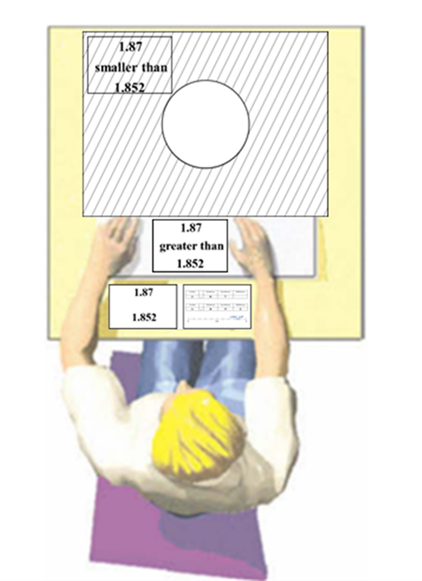
Figure 3 : The "Trap-catcher"
3. How did we prove the efficacy of this intervention ?
We used a classical method in the psychology of learning: evaluation (pretest)- intervention- evaluation (posttest). As such, before offering a pedagogical intervention, we evaluated the decimal comparison ability (pretest) of grade 3 and grade 4 students. We then randomly distributed them in two equal groups:
- A group that followed the meta-executive learning presented above.
- A group that followed a different learning (control condition). Over the course of this pedagogical intervention, we taught children the rule to follow when comparing decimal numbers (the algorithm). We thus started the intervention directly at phase 2 (presented above). In phase 3 of the intervention, the manipulation phase, participants do not use the trap-catcher, but only a simple paper separated by a line. Participants are invited to place the correct answer card above the line and the incorrect answer card below the line.
Two weeks after the intervention, we evaluated the participants’ ability to compare decimal numbers again (posttest). It was found that students that underwent a meta-executive learning progressed more between the pretest and the posttest than students in the control group. Therefore, we demonstrated the efficacy of a pedagogical approach that consists of teaching students to identify the trap and to inhibit misleading heuristics [11].
At LaPsyDÉ, we are continuing our work in order to show that this intervention can be successfully applied to other situations in school learning for which a misleading heuristic is at the source of reasoning errors. For example, in:
- Arithmetic word problems [12], 7 to 10 year-olds are taught to inhibit the “add if more or subtract if less” misconception when they resolve problems such as “Peter has 25 marbles. He has 5 less marbles than Luc. How many marbles does Luc have?”.
- Number conservation [13], 4 to 6 year-olds are taught to inhibit the “length equals number” misconception in order to successfully resolve the classical Piagetian number conservation task.
- The comparison of fractions, 4th and 5th graders are taught to inhibit the “greater the whole number, the greater the fraction” misconception when comparing fractions with common numerators (ex : 1/7 vs 1/3).
- Grammatical sentences in French.
To go further:
[1] Organization for Economic Co-operation and Development (2003). The PISA 2003 assessment framework-mathematics, reading, science and problem-solving knowledge and skills. Paris: Author.
[2] 21 du LaPsyDÉ. (2021). Développer son attention vers le nombre https://www.le21dulapsyde.com/post/d%C3%A9velopper-son-attention-vers-le-nombre
[3] 21 du LaPsyDÉ. (2021). Comment mon cerveau apprend-il les mathématiques ?. https://www.le21dulapsyde.com/post/comment-mon-cerveau-apprend-il-les-mathématiques
[4] Houdé, O., Pineau, A., Leroux, G., Poirel, N., Perchey, G., Lanoë, C., Lubin, A., Turbelin, M.R., Rossi, S., Simon, G. and Delcroix, N., 2011. Functional magnetic resonance imaging study of Piaget’s conservation-of-number task in preschool and school-age children: A neo-Piagetian approach. Journal of experimental child psychology, 110(3), pp.332-346.
[5] Vamvakoussi, X., & Vosniadou, S. (2010). How many decimals are there between two fractions? Aspects of secondary school students’ understanding of rational numbers and their notation. Cognition and instruction, 28(2), 181-209.
[6] Roell, M., Viarouge, A., Hilscher, E., Houdé, O., & Borst, G. (2019). Evidence for a visuospatial bias in decimal number comparison in adolescents and in adults. Scientific reports, 9(1), 1-9.
[7] Rossi, S., Vidal, J., Letang, M., Houdé, O., & Borst, G. (2019). Adolescents and Adults Need Inhibitory Control to Compare Fractions. PsychArchives. https://doi.org/10.23668/psycharchives.2381
[8] Lubin, A., Rossi, S., Lanoë, C., Vidal, J., Houdé, O., & Borst, G. (2016). Expertise, inhibitory control and arithmetic word problems: A negative priming study in mathematics experts. Learning and Instruction, 45, 40-48.
[9] Houdé, O. (2019). 3-system theory of the cognitive brain: A post-Piagetian approach to cognitive development. Routledge.
[10] Houdé, O. et al. Shifting from the perceptual brain to the logical brain: the neural impact of cognitive inhibition training. J. Cogn. Neurosci. 12, 721–728 (2000).
[11] Hilscher, E., Létang, M., Roell, M., Viarouge, A., Houdé, O., & Borst, G. (en révision). Improving decimal number comparison in school-age children by teaching how to inhibit a misleading strategy. Science of learning.
[12] Létang, M., Citron, P. Garbarg-Chenon, J., Houdé, O., & Borst, G. (en revision). Learning to inhibit a misleading strategy to overcome difficulties with arithmetic word problems in the classroom : Converging evidence from a laboratory and citizen research studies. Learning and instructions.
[13] Létang, M. & Garbarg-Chenon, J. (2020). Entraîner le cerveau à résister – Coffret Non-lecteurs. Nathan
Authors :

Margot Roell
Postdoctoral fellow at LaPsyDÉ, University of Paris

Emma Hilscher
PhD student at LaPsyDÉ, University of Paris
É

Grégoire Borst
Director of LaPsyDÉ & Full Professor of developmental psychology and cognitive neuroscience of education, University of Paris




Commentaires